Mirrors/hacktricks
2
0
Fork 0
mirror of https://github.com/carlospolop/hacktricks synced 2024-11-25 22:20:43 +00:00
Code Issues Projects Releases Packages Wiki Activity
hacktricks/crypto-and-stego/padding-oracle-priv.md

11 KiB
Raw Blame History

Padding Oracle

{% hint style="success" %} Learn & practice AWS Hacking:HackTricks Training AWS Red Team Expert (ARTE)
Learn & practice GCP Hacking: HackTricks Training GCP Red Team Expert (GRTE)

Support HackTricks
{% endhint %}

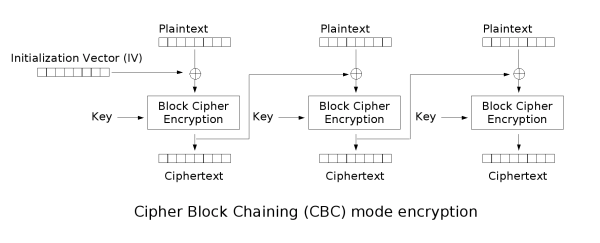
CBC - Cipher Block Chaining

In CBC mode the previous encrypted block is used as IV to XOR with the next block:

https://defuse.ca/images/cbc_encryption.png

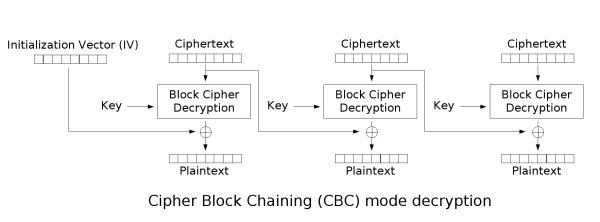
To decrypt CBC the opposite operations are done:

https://defuse.ca/images/cbc_decryption.png

Notice how it's needed to use an encryption key and an IV.

Message Padding

As the encryption is performed in fixed size blocks, padding is usually needed in the last block to complete its length.
Usually PKCS7 is used, which generates a padding repeating the number of bytes needed to complete the block. For example, if the last block is missing 3 bytes, the padding will be \x03\x03\x03.

Let's look at more examples with a 2 blocks of length 8bytes:

byte #0 byte #1 byte #2 byte #3 byte #4 byte #5 byte #6 byte #7 byte #0 byte #1 byte #2 byte #3 byte #4 byte #5 byte #6 byte #7
P A S S W O R D 1 2 3 4 5 6 0x02 0x02
P A S S W O R D 1 2 3 4 5 0x03 0x03 0x03
P A S S W O R D 1 2 3 0x05 0x05 0x05 0x05 0x05
P A S S W O R D 0x08 0x08 0x08 0x08 0x08 0x08 0x08 0x08

Note how in the last example the last block was full so another one was generated only with padding.

Padding Oracle

When an application decrypts encrypted data, it will first decrypt the data; then it will remove the padding. During the cleanup of the padding, if an invalid padding triggers a detectable behaviour, you have a padding oracle vulnerability. The detectable behaviour can be an error, a lack of results, or a slower response.

If you detect this behaviour, you can decrypt the encrypted data and even encrypt any cleartext.

How to exploit

You could use https://github.com/AonCyberLabs/PadBuster to exploit this kind of vulnerability or just do

sudo apt-get install padbuster

Για να δοκιμάσετε αν το cookie μιας ιστοσελίδας είναι ευάλωτο, θα μπορούσατε να δοκιμάσετε:

perl ./padBuster.pl http://10.10.10.10/index.php "RVJDQrwUdTRWJUVUeBKkEA==" 8 -encoding 0 -cookies "login=RVJDQrwUdTRWJUVUeBKkEA=="

Encoding 0 σημαίνει ότι χρησιμοποιείται το base64 (αλλά υπάρχουν και άλλες επιλογές, ελέγξτε το μενού βοήθειας).

Μπορείτε επίσης να καταχραστείτε αυτήν την ευπάθεια για να κρυπτογραφήσετε νέα δεδομένα. Για παράδειγμα, φανταστείτε ότι το περιεχόμενο του cookie είναι "user=MyUsername", τότε μπορείτε να το αλλάξετε σε "_user=administrator_" και να κλιμακώσετε τα δικαιώματα μέσα στην εφαρμογή. Μπορείτε επίσης να το κάνετε χρησιμοποιώντας το paduster καθορίζοντας την παράμετρο -plaintext:

perl ./padBuster.pl http://10.10.10.10/index.php "RVJDQrwUdTRWJUVUeBKkEA==" 8 -encoding 0 -cookies "login=RVJDQrwUdTRWJUVUeBKkEA==" -plaintext "user=administrator"

Αν ο ιστότοπος είναι ευάλωτος, το padbuster θα προσπαθήσει αυτόματα να βρει πότε συμβαίνει το σφάλμα padding, αλλά μπορείτε επίσης να υποδείξετε το μήνυμα σφάλματος χρησιμοποιώντας την παράμετρο -error.

perl ./padBuster.pl http://10.10.10.10/index.php "" 8 -encoding 0 -cookies "hcon=RVJDQrwUdTRWJUVUeBKkEA==" -error "Invalid padding"

Η θεωρία

Συνοπτικά, μπορείτε να ξεκινήσετε την αποκρυπτογράφηση των κρυπτογραφημένων δεδομένων μαντεύοντας τις σωστές τιμές που μπορούν να χρησιμοποιηθούν για να δημιουργήσουν όλα τα διαφορετικά padding. Στη συνέχεια, η επίθεση padding oracle θα αρχίσει να αποκρυπτογραφεί τα bytes από το τέλος προς την αρχή μαντεύοντας ποια θα είναι η σωστή τιμή που δημιουργεί ένα padding 1, 2, 3, κ.λπ.

Φανταστείτε ότι έχετε κάποιο κρυπτογραφημένο κείμενο που καταλαμβάνει 2 blocks που σχηματίζονται από τα bytes από E0 έως E15.
Για να αποκρυπτογραφήσετε το τελευταίο block (E8 έως E15), ολόκληρο το block περνάει από την "αποκρυπτογράφηση block cipher" παράγοντας τα ενδιάμεσα bytes I0 έως I15.
Τέλος, κάθε ενδιάμεσο byte XORed με τα προηγούμενα κρυπτογραφημένα bytes (E0 έως E7). Έτσι:

  • C15 = D(E15) ^ E7 = I15 ^ E7
  • C14 = I14 ^ E6
  • C13 = I13 ^ E5
  • C12 = I12 ^ E4
  • ...

Τώρα, είναι δυνατόν να τροποποιήσετε το E7 μέχρι το C15 να είναι 0x01, το οποίο θα είναι επίσης ένα σωστό padding. Έτσι, σε αυτή την περίπτωση: \x01 = I15 ^ E'7

Έτσι, βρίσκοντας το E'7, είναι δυνατόν να υπολογίσετε το I15: I15 = 0x01 ^ E'7

Το οποίο μας επιτρέπει να υπολογίσουμε το C15: C15 = E7 ^ I15 = E7 ^ \x01 ^ E'7

Γνωρίζοντας το C15, τώρα είναι δυνατόν να υπολογίσουμε το C14, αλλά αυτή τη φορά με brute-forcing το padding \x02\x02.

Αυτή η BF είναι εξίσου περίπλοκη με την προηγούμενη καθώς είναι δυνατόν να υπολογιστεί το E''15 του οποίου η τιμή είναι 0x02: E''7 = \x02 ^ I15 οπότε χρειάζεται απλώς να βρείτε το E'14 που παράγει ένα C14 ίσο με 0x02.
Στη συνέχεια, κάντε τα ίδια βήματα για να αποκρυπτογραφήσετε το C14: C14 = E6 ^ I14 = E6 ^ \x02 ^ E''6

Ακολουθήστε αυτή την αλυσίδα μέχρι να αποκρυπτογραφήσετε ολόκληρο το κρυπτογραφημένο κείμενο.

Ανίχνευση της ευπάθειας

Εγγραφείτε και συνδεθείτε με αυτόν τον λογαριασμό.
Αν συνδεθείτε πολλές φορές και πάντα λαμβάνετε το ίδιο cookie, πιθανότατα υπάρχει κάτι λάθος στην εφαρμογή. Το cookie που επιστρέφεται θα πρέπει να είναι μοναδικό κάθε φορά που συνδέεστε. Αν το cookie είναι πάντα το ίδιο, πιθανότατα θα είναι πάντα έγκυρο και δεν θα υπάρχει τρόπος να το ακυρώσετε.

Τώρα, αν προσπαθήσετε να τροποποιήσετε το cookie, μπορείτε να δείτε ότι λαμβάνετε ένα σφάλμα από την εφαρμογή.
Αλλά αν κάνετε BF το padding (χρησιμοποιώντας το padbuster για παράδειγμα) καταφέρετε να αποκτήσετε ένα άλλο cookie έγκυρο για έναν διαφορετικό χρήστη. Αυτό το σενάριο είναι πολύ πιθανό να είναι ευάλωτο στο padbuster.

Αναφορές

{% hint style="success" %} Learn & practice AWS Hacking:HackTricks Training AWS Red Team Expert (ARTE)
Learn & practice GCP Hacking: HackTricks Training GCP Red Team Expert (GRTE)

Support HackTricks
{% endhint %}