hacktricks/reversing/cryptographic-algorithms

Cryptographic/Compression Algorithms

Identifying Algorithms

If you ends in a code using shift rights and lefts, xors and several arithmetic operations it's highly possible that it's the implementation of a cryptographic algorithm. Here it's going to be showed some ways to identify the algorithm that it's used without needing to reverse each step.

API functions

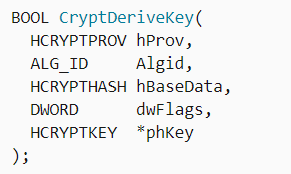
CryptDeriveKey

If this function is used, you can find which algorithm is being used checking the value of the second parameter:

Check here the table of possible algorithms and their assigned values: https://docs.microsoft.com/en-us/windows/win32/seccrypto/alg-id

RtlCompressBuffer/RtlDecompressBuffer

Compresses and decompresses a given buffer of data.

CryptAcquireContext

The CryptAcquireContext function is used to acquire a handle to a particular key container within a particular cryptographic service provider CSP. This returned handle is used in calls to CryptoAPI functions that use the selected CSP.

CryptCreateHash

Initiates the hashing of a stream of data. If this function is used, you can find which algorithm is being used checking the value of the second parameter:

Check here the table of possible algorithms and their assigned values: https://docs.microsoft.com/en-us/windows/win32/seccrypto/alg-id

Code constants

Sometimes it's really easy to identify an algorithm thanks to the fact that it needs to use a special and unique value.

If you search for the first constant in Google this is what you get:

Therefore, you can assume that the decompiled function is a sha256 calculator.
You can search any of the other constants and you will obtain probably the same result.

data info

If the code doesn't have any significant constant it may be loading information from the .data section.
You can access that data, group the first dword and search for it in google as we have done in the section before:

In this case, if you look for 0xA56363C6 you can find that it's related to the tables of the AES algorithm.

RC4 (Symmetric Crypt)

Characteristics

It's composed of 3 main parts:

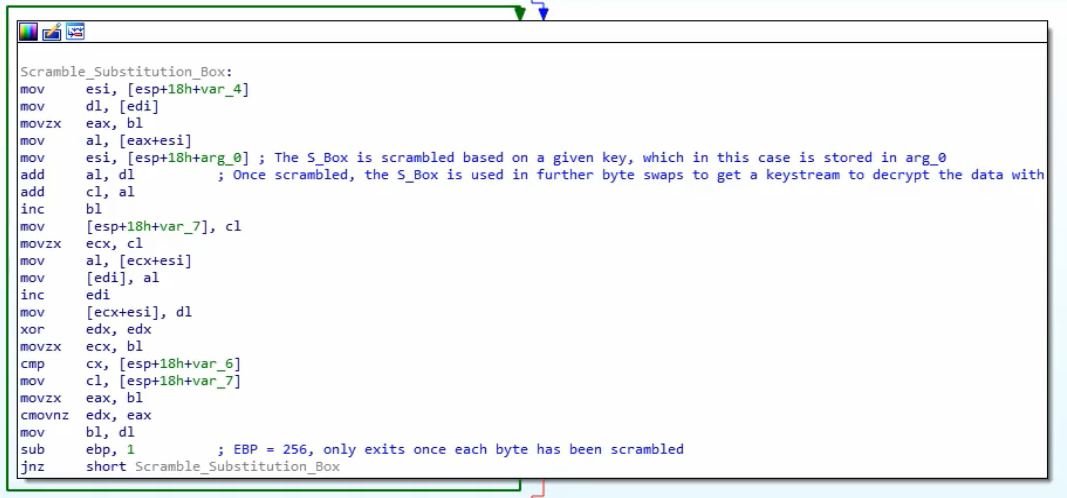
• Initialization stage/: Creates a table of values from 0x00 to 0xFF 256bytes in total, 0x100. This table is commonly call Substitution Box or SBox.
• Scrambling stage: Will loop through the table crated before loop of 0x100 iterations, again creating modifying each value with semi-random bytes. In order to create this semi-random bytes, the RC4 key is used. RC4 keys can be between 1 and 256 bytes in length, however it is usually recommended that it is above 5 bytes. Commonly, RC4 keys are 16 bytes in length.
• XOR stage: Finally, the plain-text or cyphertext is XORed with the values created before. The function to encrypt and decrypt is the same. For this, a loop through the created 256 bytes will be performed as many times as necessary. This is usually recognized in a decompiled code with a %256 (mod 256).

{% hint style="info" %} In order to identify a RC4 in a disassembly/decompiled code you can check for 2 loops of size 0x100 with the use of a key and then a XOR of the input data with the 256 values created before in the 2 loops probably using a %256 (mod 256) {% endhint %}

Initialization stage/Substitution Box: Note the number 256 used as counter and how a 0 is written in each place of the 256 chars

Scrambling Stage:

XOR Stage:

AES (Symmetric Crypt)

Characteristics

• Use of substitution boxes and lookup tables
  • It's possible to distinguish AES thanks to the use of specific lookup table values constants. Note that the constant can be stored in the binary or created dynamically.
• The encryption key must be divisible by 16 usually 32B and usually an IV of 16B is used.

SBox constants

Serpent (Symmetric Crypt)

Characteristics

• It's rare to find some malware using it but there are examples Ursnif
• Simple to determine if an algorithm is Serpent or not based on it's length extremely long function

Identifying

In the following image notice how the constant 0x9E3779B9 is used note that this constant is also used by other crypto algorithms like **TEA** -Tiny Encryption Algorithm.
Also note the size of the loop **132** and the number of XOR operations in the disassembly instructions and in the code example:

As it was mentioned before, this code can be visualized inside any decompiler as a very long function as there aren't jumps inside of it. The decompiled code can look like the following:

Therefore, it's possible to identify this algorithm checking the magic number and the initial XORs, seeing a very long function and comparing some instructions of the long function with an implementation like the shift left by 7 and the rotate left by 22.

RSA (Asymmetric Crypt)

Characteristics

• More complex than symmetric algorithms
• There are no constants! custom implementation are difficult to determine
• KANAL a crypto analyzer fails to show hints on RSA ad it relies on constants.

Identifying by comparisons

• In line 11 left there is a +7) >> 3 which is the same as in line 35 right: +7) / 8
• Line 12 left is checking if modulus_len < 0x040 and in line 36 right it's checking if inputLen+11 > modulusLen

MD5 & SHA hash

Characteristics

• 3 functions: Init, Update, Final
• Similar initialize functions

Identify

Init

You can identify both of them checking the constants. Note that the sha_init has 1 constant that MD5 doesn't have:

MD5 Transform

Note the use of more constants

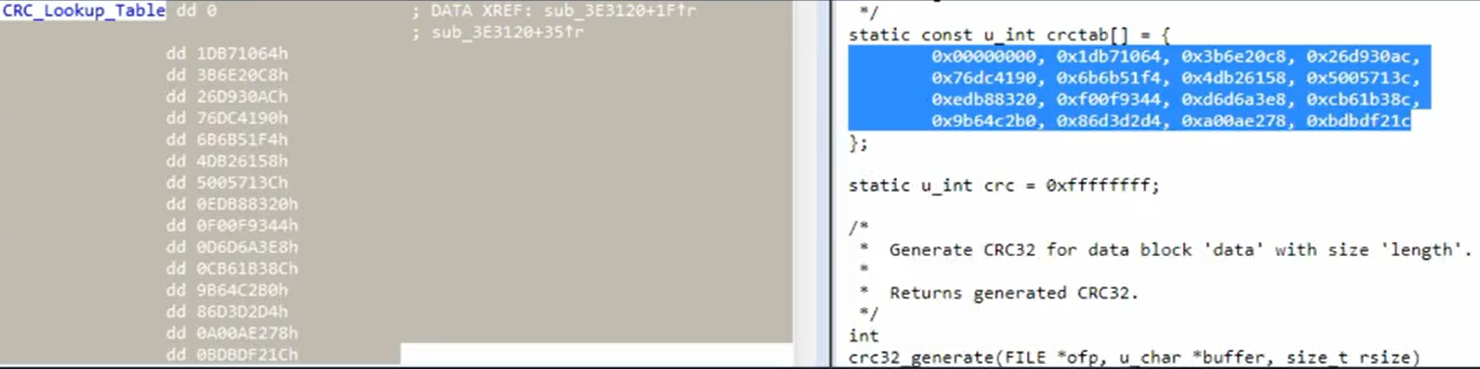
CRC hash

• Smaller and more efficient as it's function is to find accidental changes in data
• Uses lookup tables so you can identify constants

Identify

Check lookup table constants:

A CRC hash algorithm looks like:

APLib Compression

Characteristics

• Not recognizable constants
• You can try to write the algorithm in python and search for similar things online

Identify

The graph is quiet large:

Check 3 comparisons to recognise it: