# Regular expression Denial of Service - ReDoS

## Introduction

**Copied from** [**https://owasp.org/www-community/attacks/Regular\_expression\_Denial\_of\_Service\_-\_ReDoS**](https://owasp.org/www-community/attacks/Regular\_expression\_Denial\_of\_Service\_-\_ReDoS)****

The **Regular expression Denial of Service (ReDoS)** is a [Denial of Service](https://owasp.org/www-community/attacks/Denial\_of\_Service) attack, that exploits the fact that most Regular Expression implementations may reach extreme situations that cause them to work very slowly (exponentially related to input size). An attacker can then cause a program using a Regular Expression to enter these extreme situations and then hang for a very long time.

### Description

#### The problematic Regex naïve algorithm <a href="#the-problematic-regex-naive-algorithm" id="the-problematic-regex-naive-algorithm"></a>

The Regular Expression naïve algorithm builds a [Nondeterministic Finite Automaton (NFA)](https://en.wikipedia.org/wiki/Nondeterministic\_finite\_state\_machine), which is a finite state machine where for each pair of state and input symbol there may be several possible next states. Then the engine starts to make transition until the end of the input. Since there may be several possible next states, a deterministic algorithm is used. This algorithm tries one by one all the possible paths (if needed) until a match is found (or all the paths are tried and fail).

For example, the Regex `^(a+)+$` is represented by the following NFA:

![Nondeterministic Finite Automaton](https://owasp.org/www-community/assets/images/attacks/NFA.png)

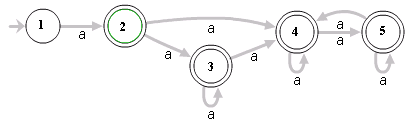
For the input `aaaaX` there are 16 possible paths in the above graph. But for `aaaaaaaaaaaaaaaaX` there are 65536 possible paths, and the number is double for each additional `a`. This is an extreme case where the naïve algorithm is problematic, because it must pass on many many paths, and then fail.

Notice, that not all algorithms are naïve, and actually Regex algorithms can be written in an efficient way. Unfortunately, most Regex engines today try to solve not only “pure” Regexes, but also “expanded” Regexes with “special additions”, such as back-references that cannot be always be solved efficiently (see **Patterns for non-regular languages** in [Wiki-Regex](https://en.wikipedia.org/wiki/Regular\_expression) for some more details). So even if the Regex is not “expanded”, a naïve algorithm is used.

#### Evil Regexes <a href="#evil-regexes" id="evil-regexes"></a>

A Regex is called “evil” if it can stuck on crafted input.

**Evil Regex pattern contains**:

* Grouping with repetition
* Inside the repeated group:
  * Repetition
  * Alternation with overlapping

**Examples of Evil Patterns**:

* `(a+)+`
* `([a-zA-Z]+)*`
* `(a|aa)+`
* `(a|a?)+`
* `(.*a){x} for x \> 10`

All the above are susceptible to the input `aaaaaaaaaaaaaaaaaaaaaaaa!` (The minimum input length might change slightly, when using faster or slower machines).

## Examples

```javascript
function check_time_regexp(regexp, text){
    var t0 = new Date().getTime();;
    new RegExp(regexp).test(text);
    var t1 = new Date().getTime();;
    console.log("Regexp " + regexp + " took " + (t1 - t0) + " milliseconds.")
}


[
//  "((a+)+)+$",  //Eternal,
//  "(a?){100}$", //Eternal
    "(a|a?)+$",
    "(\\w*)+$",   //Generic
    "(a*)+$",
    "(.*a){100}$",
    "([a-zA-Z]+)*$", //Generic
    "(a+)*$",
].forEach(regexp => check_time_regexp(regexp, "aaaaaaaaaaaaaaaaaaaaaaaaaa!"))

/*
Regexp (a|a?)+$ took 5076 milliseconds.
Regexp (\w*)+$ took 3198 milliseconds.
Regexp (a*)+$ took 3281 milliseconds.
Regexp (.*a){100}$ took 1436 milliseconds.
Regexp ([a-zA-Z]+)*$ took 773 milliseconds.
Regexp (a+)*$ took 723 milliseconds.
*/
```

## Tools

{% embed url="https://github.com/doyensec/regexploit" %}